31. Active appearance model
ASM(Active appearance model)은 새로운 이미지에서 원하는 물체를 찾기 위해 데이터의 반복적인 변형을 통해 원하는 물체를 찾아내는 통계적 모델이다. 능동 형태 모형(ASM)은 얼굴 이미지 분석이나 의료 영상 등에서 많이 사용되고 있다. 능동 형태 모형을 진행하기 위해서는 찾고 싶은 물체의 형체 데이터와 물체의 각 특징 점들이 나타내는 속성 정보가 필요하다.
찾고 싶은 물체의 모형을 알기 위해 준비된 데이터들을 통해 점 분포 모델(Point Distribution Model)을 만든다. 점 분포 모델(PDM)을 만들 때 많이 이용하는 분석 방식은 프로크루스테스 분석이다. 프로크루스테스 분석에서는 데이터의 Translation, scaling, rotation을 제거해 모든 데이터들을 정규화 시킨다.
데이터들의 평균값이 원점으로 이동시켜 데이터의 이동값을 제거하고, 각 데이터들과 원점간의 최소 제곱 거리(RMSD)가 1이 되도록 한다. 그리고 차원의 영향을 받지 않고 쉽게 계산하기 위해 SVD를 이용하여 회전값을 계산하고 제거한다.
물체의 형태 데이터를 얻었으면 새로운 이미지에서 해당 물체를 탐색한다. 이미지에서 탐색할 초기 위치를 지정한 뒤 다음의 방법을 반복한다.
1. 각 특징점에서 특징점마다 물체의 특징을 잘 나타내는 점으로 특징점을 이동한다.
2. 형태 데이터에서 얼마나 벗어나는지 확인한 뒤 형태 조건을 적용한다.
특징점에서 물체의 특징을 어떤 방식으로 추출하고, 어떤 방식으로 찾아가게 할 것인가가 ASM에서 가장 중요한 요소이다.
32. Morphology operation : Dilation, Erosion, Opening, Closing
모폴로지는 영상의 밝은 영역이나 어두운 영역을 축소, 확대하는 기법으로 영상에서 잡음을 제거하거나, 영상에서 객체의 모양을 기술하는 용도로 사용된다.
모폴로지 처리는 대상 영역이 좁아지는 침식연산(Erosion), 대상 영역이 넓어지는 팽창 연산(Dilation), 대상 영역에서 세부 영역이 제거되는 열림 연산(Opening), 빈틈이 채워지는 닫힘 연산(Closing)이 있다.
이진 영상에서 모폴로지를 살펴보면, 침식은 입력한 이진 영상의 각 픽셀에 마스크를 놓았을 때 마스크가 255값을 가지즌 모든 픽셀 위치에 대하여 입력 영상도 255값을 가져야만 결과값이 255가 되는 연산이다. 대상 위치에서 한 픽셀이라도 0값을 가지면 결과값은 0이 되기 때문에 전체적으로 255값을 가지는 영역이 줄어드는 결과가 나타난다.
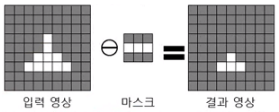
팽창 연산은 침식 연산과 반대로 마스크의 유효 영역에 있는 픽셀들을 모두 밝게 만드는 역할을 한다.
열림과 닫힘 연산은 침식과 팽창 연산을 결합한 형태로 구현할 수 있다. 열림 연산은 밝은 영역에 나타난 미세한 조각을 제거할 수 있도록 하는 연산이다. 먼저 침식 연산을 수행하여 밝은 영역을 전체적으로 축소한 다음 팽창 연산을 뒤이어 수행하여 전체적인 넓이를 원래대로 복구한다. 이러한 원리로 미세한 조각(노이즈)을 제거한다.
닫힘 연산은 밝은 영역에 생긴 미세한 틈을 메우는 역할을 한다. 먼저 팽창 연산을 수행하여 밝은 영역을 넓히고 다시 침식 연산을 수행한다. 틈새에 해당하는 영역은 팽창 연산을 통해 메워진다. 열림과 닫힘 연산을 구현하는 방법은 단순히 위에서 구현한 침식과 팽창연산을 순차적으로 수행하면 된다.
33. Epipolar geometry
Epipolar Geometry는 스테레오 비전, 즉 2-view 비전에서의 기하이다.
즉 Epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A와 영상 B의 매칭쌍들 사이의 기하학적 관계를 다루는 것이다.
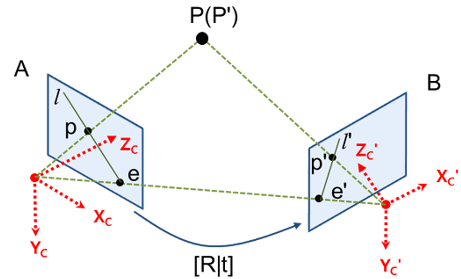
3차원 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p’에 투영되었다고 했을 때, 두 카메라 원점을 잇는 선과 이미지 평면이 만나는 점 e, e’를 epipole이라 부르고 투영점과 epipole을 잇는 직선 l, l’을 epiline(또는 epipolar line)이라 부른다. Epiline은 3차원의 점 P와 두 카메라 원점을 잇는 평면(epipolar plane)과 이미지 평면과의 교선으로도 볼 수 있다.
두 카메라 위치 사이의 기하학적 관계 [R|T]를 알고있고 영상 A에서의 영상좌표 p를 알고 있을 때, 영상 B에서 대응되는 점 p’의 좌표를 구하고자 한다. 하지만 위의 정보로 영상 B에서 대응되는 점 p’의 좌표를 유일하게 결정할 수 없다. 하지만 점 점 P는 A 카메라의 원점과 p를 잇는 직선 상에 존재하기 때문에 이 직선을 영상 B에 투영시키면 점 p’이 이 투영된 직선 위에 있음은 알 수 있다. 이 투영된 직선이 epiline l’이다.
A의 영상좌표 p로부터 대응되는 B의 영상좌표 p’을 유일하게 결정할 수는 없지만 p’이 지나는 직선인 epiline l’은 유일하게 결정할 수 있다.
한 영상좌표로부터 다른 영상에서의 대응되는 epiline을 계산해주는 변환행렬이 Fundamental Matrix, Essential Matrix이다.
34. Fundamental matrix and Essential matrix
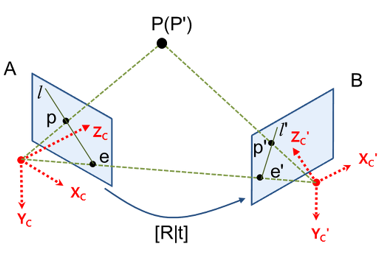
스테레오 비전에서 3차원 공간상의 한점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p’에 투영됐을 때, 두 영상 좌표 p와 p’ 사이에는 다음 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심이다.
Essential Matrix
Essential Matrix란 정규화된 이미지 평면에서의 매칭 쌍들 사이의 기하학적 관계를 설명하는 행렬이다. 즉 카메라 내부 파라미터 행렬인 k가 제거된 좌표계에서의 변환행렬이다.
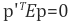
임의의 두 지점에서 찍은 영상의 매칭점들은 항상 위의 식을 통해 관계지을 수 있으며, 이 때 이 식을 epipolar constraint , 이 3x3 행렬 E를 Essential matrix 라 부른다.
Fundamental matrix
Fundamental matrix란 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀 좌표 사이의 기하학적 관계를 표현하는 행렬이다.
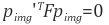
임의의 두 이미지 A, B 에 대하여, 매칭되는 픽셀 좌표 Pimg, Pimg’ 사이에는 항상 다음과 같은 관계를 만족하는 행렬 F가 존재하고, 이러한 행렬 F를 fundamental matrix라 부른다.
35. 8-point algorithm
Fundamental matrix는 카메라 캘리브레이션을 알 수 없는, 즉 Essential Matrix를 사용할 수 없는 경우에 이를 대신하여 사용된 카메라 사이의 correspondence 특성을 정의하는 matrix이다. 그리고 Fundamental matrix는 Epipolar Constraint와 8-point algorithm을 이용하여 구할 수 있다.
3x3 matrix인 Fundamental matrix는 8개의 corresponding points가 주어질 경우, 유일하게 결정 될 수 있다.
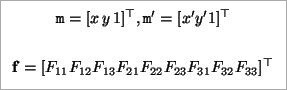
라고 했을 때, 이 vector들을 Epipolar Constraint에 대입하여 정리하면,

위 식을 이용하여 아래의 식을 생성한다.
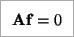
이때, A는 8개의 corresponding point pair를 이용하여 만든 matrix이다. 위 식에 의해, f는 A에 SVD(Singular Value Decomposition)를 적용하여 구할 수 있다.
36. 3-point algorithm (P3P)
월드 좌표계 상에서의 좌표를 알고있는 3차원 점들이 영상에 투영된 위치를 알면 월드 좌표계 상에서의 영상의 위치를 알아낼 수 있다. 대표적인 예로 3-point algorithm(P3P)이 있다.
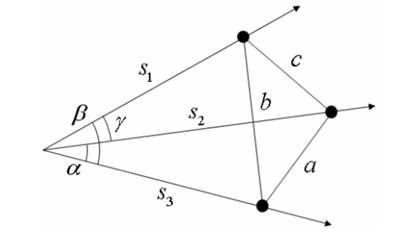
P3P 알고리즘은 3개의 점 사이의 거리 a, b, c, 그리고 이 점들이 투영된 위치로부터 계산한 카메라 광선 사이의 각도 α, β, γ를 알고 있을 때, 카메라 좌표계의 중심으로부터 각 점들까지의 거리 s1, s2, s3를 구하는 알고리즘이다.
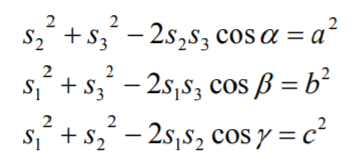
위 그림에 코사인 제 2 법칙을 이용하여 3개의 식을 얻고, 연립방정식의 해를 구하여 s1, s2, s3를 구한다.
37. Bundle adjustment
Bundle adjustment 란 앱 상의 3차원 포인트들을 키프레임 이미지들에 투영시킨 위치와 해당 영상 프레임에서 실제 관측된 위치의 차이, 즉 reprojection error를 최소화시키도록 3차원 포인트의 위치 및 카메라의 위치를 최적화하는 과정을 지칭하는 용어이다. 여기서 ‘bundle’이라는 용어는 우리말로 번역하면’묶음’이라는 의미인데, 한 포인트에 대한 reprojection error가 아니라 여러 포인트들의(그리고 여러 카메라 시점에 대한) reprojection error를 (묶음으로) 동시에 최소화시킴을 나타낸다.
3D 구조와 카메라 영상을 재 구성하기 위해 3차원 구조와 카메라 포즈를 사용하고 일반적으로 3D 지형과 카메라 포즈의 기존 추정치를 정제하기 위해 사용된다. 위치 추정 개선이 목적이다.
스테레오 영상의 경우 다른 이미지에 현재 이미지와 일치하는 형상이 있을 수 있다. 한 지점 또는 지형좌표는 x,y,z로 표현되고 하나의 노드는 카메라 포즈와 매개변수에 대한 정보가 들어있다. 카메라 포즈는 6개의 파라미터로 표현된다.(x,y,z, 회전에 관한 파라미터 3개)
한 지점 또는 지형 좌표는 카메라 포즈가 반영된 영상에서 찍히는 한 점을 의미한다.
38. Stereo rectification
스테레오 카메라 캘리브레이션이 완료되면 epipole의 위치를 알 수 있고 왼쪽 카메라 한 점에 대응되는 오른쪽 카메라 영상의 epipolar line을 알 수 있다. 일반적인 스테레오 카메라에서는 아래 그림처럼 에피폴라 라인이 사선으로 나타나게 된다.

왼쪽 카메라의 한 점에 대응되는 오른쪽 카메라의 매칭되는 점이 해당하는 epipolar line 위에 있어 그 위에 이미지 값을 확인하여 매칭되는 점을 찾으면 매칭 문제는 해결이 가능하다. 하지만 두 영상의 epipolar line이 평행선이 아니어서 일일히 다음 점의 위치를 찾아 이미지 값을 확인해야 하는식으로 프로그래밍이 된다.
이 문제를 좀 더 단순화하기 위해 epipolar line이 평행하도록 두 이미지를 변환하는 과정을 stereo rectification이라 한다. 이미지에서 캘리브레이션 데이터를 이용하여 stereo rectification한 결과는 아래와 같다.

Rectification 과정을 거치면 왼쪽 영상의 한 점은 오른쪽에서 한 줄만 처음에서부터 끝까지 찾으면 되기에 프로그래밍이 간결해 진다. rectification하는데 시간이 추가로 소요되지만 매칭에 줄어드는 시간까지 함께 생각해보면 rectification을 수행하는 쪽이 훨씬 빠르기에 스테레오 매칭에 있어서 rectification은 필요한 과정으로 인식되고 있다.
39. Image stitching
Image stitching이란 여러 장의 사진을 자연스럽게 이어 붙여 하나의 커다란 이미지로 결합하는 기술을 말한다. Image stitching의 예로 파노라마 사진 기술이나 360도 카메라가 있다.
Image stitching은 이미지 등록, 이미지 캘리브레이션, 그리고 이미지 블랜딩 이렇게3단계로 구성되어 있다.
이미지 등록(image registration)
중첩 픽셀들 간의 차이가 최소가 되는 조건으로 여러 이미지들을 인접한 순서대로 정렬하여 매칭하는 과정이다. 일반적으로 컴퓨터비전에서 많이 활용되는 RANSAC 반복법에 의한 알고리즘을 사용한다.
이미지 캘리브레이션(image calibration)
개개의 요소사진을 조작하여 변환시키는 과정이다. 인접 사진의 중첩 영역에서 발생한 차이들 즉, 카메라 렌즈의 색수차, 왜곡수차, 비네팅 등과 같은 광학적인 결함에 의해서 일어난 차이나 촬영시에 발생한 노출 차이 혹은 바람이나 진동같은 외부환경의 영향에 의해서 만들어진 차이를 줄이는데 목표를 둔다.
이미지 블랜딩(image blending)
이음선 부분이 나타나지 않게 중첩영역을 하나로 합성하는 과정이고 노출의 차이를 보상하기 위해 전체적인 색조정도 동시에 진행된다.
40. Background modeling for video
상황
1. 동적으로 변하는 배경
2. 서서히 변하는 조도
3. 갑자기 변하는 조도
4. 배경인 물체의 움직임
* 배경모델링 기법
1. 혼합 정규 모델
주어진 영상의 픽셀 정보들을 여러 개의 정규 분포로 모델링한 후 현재 픽셀의 배경확률로부터 배경/전경 여부를 판정

2. 코드북 기반의 배경 추출 방법
동일한 위치의 픽셀들의 정보를 코드워드에 기록한 후, 해당 픽셀에 대한 코드 워드가 존재하는지에 따라 배경/전경 여부를 판정하는 방법
3. 통계 모델링 기반의 배경 추출 방법

4. 최대 빈도 영상을 구하는 방법

'DeepLearning' 카테고리의 다른 글
| [캐글 Kaggle] 캐글 에러 - Unable to find the required key value error 해결 방법 (0) | 2021.08.17 |
|---|---|
| [DeepLearning] DeepFake(deepfacelab) 구글 Colab에서 개발하기 (2) | 2021.08.01 |
| Computer Vision Summary | 컴퓨터 비전 총정리 -3 (0) | 2021.07.12 |
| Deep Learning | GAN (Generative Adversarial Network) (0) | 2021.07.05 |
| Deep Learning | Autoencoder (0) | 2021.07.05 |




댓글