21. TOF camera
TOF는 Time Of Flight로 비행시간, 즉, 빛을 쏘아서 반사되어 돌아오는 시간을 측정하여 거리를 계산하는 방식을 말한다. TOF 카메라는 TOF 방식을 사용하여 거리(depth) 이미지를 출력해 주는 카메라를 말한다. 거리를 측정하기 위해 인위적으로 빛을 쏘는데, 이러한 방식을 active light source 방식이라고 한다. TOF의 가장 핵심적인 원리는 LED 발신부에서는 빛을 쏠 때 굉장히 빠른 간격으로 점멸을 시키면서, 즉, modulation을 시키면서 쏘고 수신부에서는 이 modulation 간격과 동기화하여 receptor들을 활성화 시키는 것이다. 여기서 LED를 켜는 동안은 in phase라 부르고 LED를 끄는 동안을 out phase라고 부른다. TOF 카메라의 이미지 센서는 각각의 셀이 in phase receptor와 out phase receptor 쌍으로 구성되어 있는데, in phase receptor는 in phase에만 활성화되어 빛을 감지하고, out phase receptor는 out phase에만 활성화되어 빛을 감지한다.

이와 같이 in phase receptor들과 out phase receptor 들을 시간차를 두고 서로 다르게 활성화 시키면 사물과의 거리에 따라서 수신되는(누적되는) 빛의 양에 차이가 발생한다. 이 차이, 즉, in phase receptor에 수신된 빛의 양과 out phase receptor에 수신된 빛의 양의 차이를 비교하여 사물과의 거리를 측정하는게 TOF 카메라의 기본 원리이다.
거리가 0인 경우에는 in phase receptor에만 빛이 수신된다. 그리고 사물과의 거리가 점점 멀어지면 in phase receptor에 수신되는 빛의 양은 줄어들고 out phase receptor에 수신되는 빛의 양은 증가한다. 그러다가 어느 순간에는 out phase receptor에만 빛이 수신된다.

여기서 d는 한 펄스 동안 빛이 이동하는 거리의 1/2로서 d=빛의 속도xmodulation 간격/2로 계산할 수 있다.(빛은 사물까지 갔다 되돌아오기 때문에 실제 사물까지의 거리는 빛의 이동거리/2 이다)
이 기본 원리를 바탕으로 추가적으로 여러 기법들이 사용된다. 거리 d를 전후로 수신 특성이 대칭되는 모호성(ambiguity) 문제를 해결하기 위해 receptor 활성화 주기를 LEB 점멸 주기와 약간 어긋나게(shift) 하거나 수신 특성이 2d를 주기로 반복되는 문제를 해결하기 위해 한 영상 프레임을 획득하는 동안 서로 다른 두 종류의 점멸 주기를 사용하는 등의 기법들이 사용된다.
TOF 카메라의 특징은 거리 분해능이 뛰어나고 정확한 반면 측정 거리가 제한적이고 실내에서만 사용이 가능하다. TOF 카메라는 각각의 receptor 쌍 마다 즉, 이미지 센서 셀마다 프로세싱 칩이 들어가기 때문에 비교적 셀의 크기가 크다. 이로 인해 TOF 카메라에 들어가는 이미지 센서의 크기가 커지거나 이미지 센서의 해상도가 낮아지는 문제가 있다.
TOF 카메라의 원리
최근에 TOF 카메라의 원리에 대해 배울 기회가 있어서 그 동안 궁금했던 TOF 방식에 대해 알게 되었습니다. 이번에 MS에서 새로 발표한 키넥트 2가 기존의 IR 구조광 방식을 버리고 TOF 방식을 사용
darkpgmr.tistory.com
22. Kinect
키넥트의 깊이 정보 추출 원리는 적외선 카메라의 중심점을 원점으로 하여 객체를 3차원으로 표시한다. Z축은 영상 영역(image plane)에 수직이고, X축은 Z축에 대하여 수직이며, 적외선 카메라에서 레이저 프로젝터로 향하는 방향이다. Y축은 Z축과 X축에 대하여 수직이다.
Kinect는 RGB 카메라의 color sensor, IR Emitter와 IR Depth sensor, 4개의 microphone array그리고 ssnsor를 상하로 움직일 수 있도록 tilt motor 등으로 구성되어 있다. 이 sensor들로 일반적인 rgb 카메라로 촬영되는 영상과 촬영된 영상의 깊이 정보를 나타내는 영상 그리고 검출된 사용자의 골격을 나타내는 영상 정보를 나타낸다.
Kinect는 RGB 영상뿐만 아니라 특정한 적외선 점 패턴을 물체에 투영하여 점 패턴의 특성을 분서하여 깊이 정보를 획득하고 스켈레톤 트랙킹을 제공한다. 키넥트 카메라는 깊이 영상 생성을 위해 물체에 반사되어 돌아오는 적외선의 패턴을 수광센서로 검출한다. 하지만 발광장치와 수광센서간의 거리 차이로 인한 사각 지대 발생, 매끄러운 물체 표면으로 인하여 적외선의 난반사가 적게 일어나 수광센서로 레이저가 돌아오지 못하는 경우에 적외선 패턴을 감지할 수 없기 때문에 검추로디지 않은 위치에 대한 값은 깊이 영상에서 홀(hole)의 형태로 나타난다.
깊이영상은 적외선 영사기에서 조사한 적외선 패턴을 적외선 카메라로 읽어 패턴 매칭 방식으로 생성한다. 깊이영상만으로 물체를 분간할 수 없어 RGB 카메라로부터 얻은 컬러영상을 동시에 이용하여 특정 픽셀의 깊이정보를 얻을 수 있다. 또한, 키넥트 센서에서는 RGB 카메라 초점거리가 적외선 카메라의 초점거리보다 짧아 컬러영상이 깊이영상보다 더 넓은 범위의 영상을 취득한다. 두 영상의 정확한 정합을 위해서는 두 영상의 초점거리를 맞추어야한다. 깊이영상의 범위를 넓혀 맞추기 위해서는 보간 기법이 추가로 필요하다.
RGB 카메라와 IR 카메라가 물리적으로 서로 떨어져 있으면 두 영상을 일치시키기 위한 조정이 필요하다는 단점이 존재한다. 인식거리가 제한적이고, 스스로 적외선을 송출하고 그것을 사용해 촬영하므로 외부조명의 영향을 비교적 적게 받으나 여전히 조명의 영향으로부터 완전히 자유롭지는 못하다.
Kinect v1의 depth 센서는 투광한 적외선 패턴을 읽기 패턴의 왜곡에서 Depth 정보를 얻는 light coding 방식을 사용한다. Kinect v2의 depth 센서는 투광한 적외선이 반사되어 돌아오는 시간에 depth 정보를 얻은 TOF 방식을 사용한다. Kinect v2에서 화각이 넓어져 틸트 모터는 탐재되지 않았다. Kinect2는 resolution이 더 높아지며 심도 취득 범위 또한 넓어진다. TOF방식을 통해 depth 정보의 정확도도 향상되었다. (Microsoft에서는 3배 더 좋다고 말한다.)
23. Canny edge detector
Canny edge detection은 5단계로 진행이 된다.
1. Smoothing
가장 먼저 노이즈 제거를 위한 스무딩(blur) 작업을 수행한다. 미분을 하게 되면 잡음에 의해 noise가 많이 생긴다. 이러한 잡음을 제거하기 위해 blur를 수행한다. Blur는 가우시안 함수가 이용되며, 가우시안 필터 마스크를 이용해 컨볼루션 연산으로 수행된다.
2. Finding gradients
두번째 단계는 경사(미분)값을 통해 edge를 찾는 단계이다. Edge를 정의하자면 image의 intensity가 급격하게 변하는 부분으로 볼 수 있다. 극 값은 maximum, minimum 2 군데를 찾을 수 있으며, 일반적으로 extrema라고 둘을 칭한다. 이렇게 extrema를 찾기 위해서 sobel mask를 이용해 컨볼루션한다. x축과 y축에 대하여 각각 미분을 하여 각각의 영상을 획득한다. 이제 가장 빠르게 증가한 방향(direction)과 강도(norm)를 구해야 한다. 피타고라스의 정리를 통해 경사 강도를 얻을 수 있다. (Euclidean distance와 달리 대각선을 고려하지 않는 Manhattan distance를 이용하는 방법도 있다.) dierection은 삼각함수를 이용해 얻는다. 소벨마스크를 통해 얻은 x축과 y축의 미분값을 가지고, 아크탄젠트를 이용해 각도 세타를 얻는다.
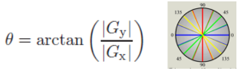
이 각도를 구한 후에 45도 간격으로 라운딩하면서 8방향으로 그룹화시킨다.
3. Non-maximum suppression
Local maxima를 선택하는 단계이다. 진짜 edge가 아님에도 불구하고 잘못 검출된 영역이 존재하는데, 이들을 제거하는 단계이다. Blur를 통해 흐려진 edge에서 잘못된 검출이 발생할 수도 있다.
이전 과정을 통해 얻은 Norm과 direction 정보를 가지고 양 방향과 음 방향으로 에지강도와 현재 픽셀의 에지 강도를 비교판단한다. 현재 픽셀의 에지 강도가 주변에 비해 가장 크다면 그 값을 보존하고 아니면 삭제하는 것이다. 4방향 혹은 8방향의 이웃을 검사하는 방법 두가지가 있다.
4. Double thresholding
위 단계를 거친 이미지에 나타나는 에지들 중에는 실제 에지와 약간의 노이즈에 의해 검출된 것들이 존재한다. 이들을 구분하기 위해 2개의 임계값을 사용한다. High threshold와 low threshold의 두 개의 threshold 값이 존재하며, high threshold 이상의 edginess를 갖는 픽셀들은 무조건 edge 픽셀로 분류한다. 그리고 low threshold 이하의 edginess를 갖는 픽셀들은 제거한다. High와 low 사이에 있는 값들은 hysteresis 방법을 이용해 구분한다.
5. Edge tracking by hysteresis
High와 low 사이에 있는 값들은 이미 edge로 분류된 픽셀들과 연결되어(인접해) 있으면 edge 픽셀로 분류하고, 나머지 픽셀들은 모두 non edge 픽셀로 분류한다. 즉, hysteresis thresholding의 요점은 판단이 확실한 경우에는 그대로 이진화(edge인지 아닌지)를 하되 그 판단이 불확실한 경우에는 주변 상황을 보고 결정하는 것이다.
24. Laplace edge detector
Laplacian edge detector는 3단계로 이루어진다.
1. Blur the image
모든 edge가 아닌, main features를 나타내는 edge만 찾고 싶다면, 영상을 blur하는 것이 도움이 된다. Gaussian filter를 이용해 blur하는 것이 일반적이다.
2. Perform the laplacian on this blurred image
왜 라플라시안을 사용하는지에 대해 설명하자면, 1차원의 예제로 보는 것이 쉽다.
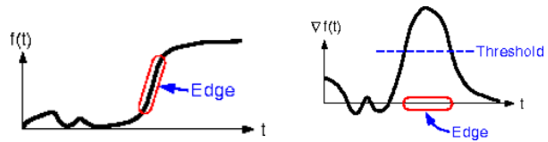
어떤 신호(좌측)에 gradient를 취하면, 오른쪽 그림과 같이 된다. 명백하게 gradient는 edge 부분에서 큰 peak 부분을 갖는다. Gradient 값이 threshold보다 높을 때를 edge로 detect할 수 있다. 그러나, threshold 때문에 edge 영역은 두껍다. Laplacian을 취하고 zero crossing을 찾음으로써 최대의 peak를 찾을 수 있다.

위의 그림은 laplacian의 결과를 보여준다. Edge는 zero crossing부분에 발견된다. 하지만, small ripples에 대응되는 zero crossing도 많이 발견되었다. local variance를 계산하고, local variance가 낮다면, ripple때문에 일어난 zero crossing이라고 판단한다.
3. Median filter the result image.
결과 영상에 많은 spot noise가 존재하기 때문에, 중간값 필터로 제거한다.
25. Kalman filter
과거의 측정 데이터(기존에 알고 있는 것)와 새로운 측정 데이터를 사용하여 새로운 결과를 추정하는데 사용하는 알고리즘으로 선형적 움직임을 가지는 대상을 재귀적 적용으로 동작시킨다. 여기서 filter는 측정 데이터에 포함된 불확실성(noise)를 필터링 하는 것을 의미한다. 확률에 기반한 예측시스템이므로 이것의 대상은 정규분포(가우시안분포)를 가지는 대상이 된다.
실제 응용에 있어서는 시스템이 비선형이고 잡음도 gaussian의 형태가 아닌 경우가 많으므로 칼만필터의 변형이 요구되며, EKF(Extended Kalman Filter)가 가장 많이 사용된다. EKF는 선형화 칼만필터(Linearized KF; LFK)와 유사하나 선형화하는 기준점을 계속 갱신해 나간다는 특징을 가지고 있다.
칼만필터의 알고리즘은 두 단계로 구성된다.
1. Propagation 단계: 현재의 상태변수 추정치 및 공분산 값으로부터 다음 측정시간에서의 상태변수 추정치 및 공분산을 계산하는 단계. 수치적으로는 시간적분에 해당하는 단계.
2. Update 한계: 새로운 측정치와 propagation으로부터 얻어진 상태변수 추정치를 혼합하여 상태변수 추정치를 새롭게 계산하는 단계. 이 단계에서 칼만필터 게인 K를 최적추정 이론에 따라 계산한다.
선형 시스템은 직접 센서들에서 측정가능한 측정모델함수(오차포함)와 현재 상태를 표현하지만 직접 측정이 불가능한 상태모델함수로 단순화시킨 두개의 식으로 표현이 가능하다.

위 식에서 y는 측정값, z는 측정잡음이며 상태모델의 x값을 이용하여 y를 확정한다. x는 시스템의 현재상태값으로 위치나 속도 등이 될 수 있고, w인 프로세서 잡음과 y를 이용하여 구할 수 있다.
실제 우리가 구하고자 하는 것은 다음 시간의 x값이다. u라는 변수엔 시스템에서 제어할 수 없는 잡음이 들어오고, 현재의 x값에 프로세서 잡음 w가 합쳐져 정해지는데 결국 현재의 x가 y와 z에 영향 받으므로, 홈 피드백이 걸린다.(?)

Xk-1은 이전 상태이며, Xk는 현상태이다. K는 칼만 게인(Kalman Gain), P는 추정오차공분산 행렬(The estimation error covariance matrix), ^는 상태변수라는 표현이고, x-의 –는 이전상태를 말한다고 보면 된다. Q는 예측노이즈 공분산, R은 측정노이즈 공분산이다.
여기서는 time update와 measurement update라는 두개의 상태로 나눠 구현되었다. 위에서 말한 상태모델함수가 time update이고, 측정모델함수가 measurement update와 같다.
초기에 X와 P를 위한 초기예측이 제공되어야 한다. 상수항인 변하지 않는 행렬 A, H, Q, R 값이 있고, 루틴을 시작하기에 앞서 초기값이 이미 있어야 한다.
Time update: 예측단계(시간갱신), 이전데이터를 근거로 예측
1. 이전상태벡터 x에 A를 곱하고 u(예측오차잡음)에 B를 곱하여 구한 X는 순수한 상태예측값이다.
2. 에러보정을 위해 수행하는 단계로 수집된 자료를 기반으로 얼마의 보정할지 결정한다. (프로세스노이즈 예측)
Measurement update: 교정단계(측정치갱신), 새로운 측정값으로 교정
1. 프로세스노이즈(예측오차분)과 측정노이즈(실측잡음분)을 이용해 칼만 게인을 구한다.
2. 측정잡음z를 추가하여 현재의 상태벡터x를 구한다.
3. 예측 오류인 추정 오차공분산 P를 구한다.
예측은 항상 오차를 보이는데, 이것은 프로세스 노이즈(process noise)라 하고, 이 프로세스노이즈와 측정노이즈를 공분산을 이용하여 가중치처리를 한다. 즉, 프로세스 노이즈가 측정 노이즈보다 분산이 크다면, 측정에 더 큰 가중치가 곱해지고, 프로세스 노이즈가 측정 노이즈보다 분산이 작다면, 모델을 이용한 예측 값에 더 큰 가중치가 곱해져 업데이트 되는 구조로 작동된다. 변하지 않는 행렬값과 초기값을 가지고 예측루틴의 값을 구하게 된다. (이후 이 값을 이용하여?) Kalman gain과 측정값 z를 이용하여 다음 예측치를 보정하고 프로세스 노이즈 분산을 보정한다. 이런 과정을 반복하여 칼만 필터는 동작한다.
공분산? Covariance? 2개의 확률변수의 상관정도를 나타내는 값이다.
만약 2개의 변수 중 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 경향의 상관관계가 있다면 공분산의 값은 양수가 된다. 반대로 2개의 변수 중 하나의 값이 상승하는 경향을 보일 때, 다른 값이 하강하는 경향을 보인다면 공분산의 값은 음수가 된다. 이렇게 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있다. Cov(x,y) > 0이면, x가 증가할 때 y도 증가하고, Cov(x,y) < 0 이면, x가 증가할 때 y는 감소하는 경향을 보인다. 두 변수가 아무 상관없이 흩어져있다면, Conv(x,y) = 0에 근접한다.

LKF는 실제환경에서는 잘 동작되지 않는 경우가 많다. 이유는 실제환경은 시스템이 선형이 아닌 비선형이고, 잡음경우도 gaussian이 아닌 경우가 많아 변형칼만필터가 요구된다. EKF가 많이 사용되며, EKF로도 부족한 부분이 많아 반복적 EKF를 사용하기도 한다. 동시에 여러 개의 가정이 필요한 모델일 경우 콘덴세이션 알고리즘(파티클 필터 기반)으로 접근한다.
26. Camshift, Meanshift
Mean-shift 알고리즘은 데이터 집합의 밀도분포(특징점, 코너, 색상)를 기반으로 관심영역(Region Of Interest; ROI) 객체를 고속으로 추적하는 알고리즘이다. 초기의 검색 영역의 크기와 위치를 지정하면 반복되는 색 분할 계산에 의해서 색상 클러스터가 발생되고, 초기 지정한 색 영역에 기반하여 경계를 결정하여 관심 물체를 추출할 수 있다. 이것을 mode seeking 알고리즘이라 고도하며, 특정 데이터들의 중심(mean)으로 이동(shift)하는 알고리즘이다. 이를 이용하여 데이터 분포의 mode를 찾기도 하고, tracking도 한다.
1. 임의로 관심영역을 잡고,
2. 선택된 범위 안에 들어있는 특징점들의 밀도가 가장 큰 곳을 찾는다.
3. 밀도가 가장 큰 곳을 중심으로 재설정 한다.
4. 재설정된 중심을 기준으로 임의의 범위를 다시 잡는다.
위 과정을 반복하는데, 이렇게 반복하면 전체에서 가장 밀도가 많은 부분에서 맴돌고 있게 된다. 이렇게 전체 영역에서 특정한 고밀도 부분, 혹은 저밀도 부분을 찾는 알고리즘이다.
Mean-shift 알고리즘의 단점은 복잡한 계산량에 의해 실시간 사용에 무리가 있다. 이런 문제를 해결하기 위해 CAMShift 방법이 사용된다.
CAMshift(Continuously Adaptive Mean Shift) 알고리즘은 color segment 방법의 meanshift 알고리즘을 streaming 환경에서 사용하기 위해 개선한 것으로 탐색윈도우의 크기를 스스로 조정하는 기법을 사용하여 mean-shift의 단점을 보강한다. 객체를 고속으로 추적하는데 사용되며, 조도변화, 잡음이 많은 배경에서는 성능이 좋지 않은 특징이 있다. 검출된 객체의 영역의 Hue 값의 분포를 이용하여 변화될 위치를 예측하고 탐지한 후 중심을 찾아 객체를 추적하게 된다. 임의의 물체를 추출하기 위해 경험적 분포(empirical distribution)에서 동작하는 탐색 알고리즘이다. 영상에서 조도의 변화는 휘도에 가장크게 나타난다. 따라서 상대적으로 Hue 값을 사용하면 조명의 영향에 덜 민감하므로 Hue값을 사용한다.
1. 관심영역이 주어지면 HSV 색 모델의 Hue 값으로 변환한다.
2. 관심영역에서 1차원 histogram을 구축하여 저작하고 추적 모델로 사용한다.
3. 탐색 윈도우에서 객체의 중심을 찾고, 물체의 중심에 탐색 윈도우를 위치시키고 영역을 찾는다. 수렴할 때까지 과정을 반복한다.
4.
영상 내에서 여러 개의 윈도우를 설정한다. 각 윈도우의 크기 및 중심점의 위치를 반복적으로 변화시키는데, 이 때 윈도우 중심점의 위치는 윈도우 내에 분류된 화소값들의 평균이 되며, 크기는 화소값들의 합에 비례해 증가한다. 이 과정을 모든 윈도우가 수렴할 때까지 반복하는데, 윈도우의 수렴 여부는 윈도우의 위치와 크기의 변화량에 의해서 결정된다. 즉, 변경된 윈도우의 위치와 크기가 이전값과 차이가 없을 때 해당 윈도우는 수렴하게 된다.
CAMShift는 경사 상승(gradient ascent) 알고리즘으로 부분적 최적해에 수렴될 수 있는데, 이를 극복하기 위해 입력 영상내에 여러 개의 윈도우를 설정하는 방법을 사용하기도 한다. Camshift는 지역적으로 윈도우를 조절하며 동작하므로 모든 영상의 화소를 분류할 필요가 없이 각 윈도우 내의 화소들만 분류하면 된다는 이점이 있다.
27. EM algorithm
EM(Expectation maximization) 알고리즘은 latent variable이 존재하는 probabilistic model의 maximum likelihood 혹은 maximum a posterior 문제를 풀기 위한 알고리즘 중 하나이다. Iterative한 알고리즘이다.
Latent variable은 임의로 설정한 hidden variable을 의미한다. Latent variable Z의 marginal distribution을 q(Z)라고 정의한다면, log-likelihood를 decompose할 수 있다.
lower bound가 maximum이 되도록 하는 θ와 q(Z) 의 값을 찾고, 그에 해당하는 log-likelihood의 값을 찾는 알고리즘을 설계하는 것이 가능할 것이다. 만약 θ와 q(Z) 를 jointly optimize하는 문제가 어려운 문제라면 이 문제를 해결하는 가장 간단한 방법은 둘 중 한 variable을 고정해 두고 나머지를 update한 다음, 나머지 variable을 같은 방식으로 update하는 alternating method일 것이다. EM 알고리즘은 이런 아이디어에서부터 시작하게 된다. EM 알고리즘은 E-step과 M-step 두 가지 단계로 구성된다. 각각의 step에서는 앞서 설명한 방법처럼 θ와 q(Z) 를 번갈아가면서 한 쪽은 고정한 채 나머지를 update한다. 이런 alternating update method는 한 번에 수렴하지 않기 때문에, EM 알고리즘은 E-step과 M-step을 알고리즘이 수렴할 때까지 반복하는 iterative 알고리즘이 된다.
현재 우리가 가지고 있는 parameter θ의 값을 θold라고 정의해보자. EM 알고리즘의 E-step은 먼저 θold 값을 고정해 두고 L(q,θ)의 값을 최대로 만드는 q(Z)의 값을 찾는 과정이다. 이 과정은 매우 간단하게 계산 수 있는데, 그 이유는 log-likelihood ln p(X|θold)의 값이 q(Z) 값과 전혀 관계가 없기 때문에, 항상 L(q,θ) 를 최대로 만드는 조건은 KL divergence가 0이 되는 상황이기 때문이다. KL divergence는 q(Z)=p(Z|X,θold) 인 상황에서 0이 되기 때문에, q(Z) 에 posterior distribution p(Z|X,θold) 을 대입하는 것으로 해결할 수 있다. 따라서 E-step은 언제나 KL-divergence를 0으로 만들고, lower bound와 likelihood의 값을 일치시키는 과정이 된다.
E-step에서 θold 을 고정하고 q(Z)에 대한 optimization 문제를 풀었으므로 M-step에서는 그 반대로, q(Z) 를 고정하고 log-likelihood를 가장 크게 만드는 새 parameter θnew을 찾는 optimization 문제를 푸는 단계가 된다. E-step에서는 update하는 variable과 log-likelihood가 서로 무관했기 때문에 log-likelihood가 증가하지 않았지만, M-step에서는 θ가 log-likelihood에 직접 영향을 미치기 때문에 log-likelihood 자체가 증가하게 된다. 또한 M-step에서 θold가 θnew로 바뀌었기 때문에 E-step에서 구했던 p(Z)p(Z)로는 더 이상 KL-divergence가 0이 되지 않는다. 따라서 다시 E-step을 진행시켜 KL-divergence를 0으로 만들고, log-likelihood의 값을 M-step을 통해 키우는 과정을 계속 반복해야만 한다.
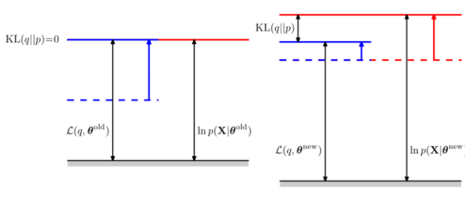
위의 그림에서 왼쪽이 E-step을 의미하고, 오른쪽 그림이 M-step을 의미한다. E-step을 의미하는 왼쪽 그림에서 KL divergence는 0이 되고, lower bound인 functional과 log-likelihood의 값이 같아진다. 오른쪽 그림은 M-step을 표현하고 있으며, θ가 update되면서 log-likelihood의 값이 증가하게 되지만, 더 이상 KL divergence의 값이 0이 아니게 된다. 이 과정을 더 이상 값이 변화하지 않을 때까지 충분히 많이 돌리게 되면 이 값은 log-likelihood의 어떤 값으로 수렴하게 될 것이다. 그리고 매 step마다 항상 optimal한 값으로 진행하기 때문에 이 값은 log-likelihood의 local optimum으로 수렴하게 된다는 사실까지 알 수 있다. EM algorithm은 아래와 같은 그림으로 표현할 수 있다.
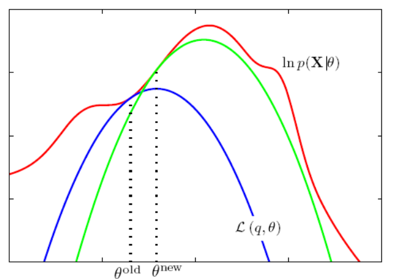
각 curve는 θ 값이 고정이 되어있을 때 q(Z)에 대한 lower bound L(q,θ)의 값을 의미한다. 매 E-step마다 고정된 θ에 대해 p(Z)를 풀게 되는데, 이는 곧 log-likelihood와 curve의 접점을 찾는 과정과 같다. 또한 M-step에서는 θ 값 자체를 현재 값보다 더 좋은 지점으로 update시켜서 curve 자체를 이동시키는 것이다. 이런 과정을 계속 반복하면 알고리즘은 언젠가 local optimum으로 수렴하게 될 것이다. Local optimum에 수렴한다는 성질은 얼핏 보면 나빠 보일 수도 있지만, 이 글의 도입부에서 latent variable이 introduce되는 이유 자체가 원래 log-likelihood를 계산하는 것이 불가능에 가깝기 때문이었다는 사실을 돌이켜본다면, latent variable을 잘 잡기만 한다면 반드시 local optimum으로 수렴하는 EM 알고리즘은 매우 훌륭한 알고리즘이라는 사실을 알 수 있다. 즉, 아예 문제를 풀지 못하는 것 보다는 local optimum으로 수렴하는 것이 훨씬 좋다.
대부분의 probabilistic model의 MLE 혹은 MAP는 EM 알고리즘을 사용하면 구할 수 있다. 그러나 EM 알고리즘이 항상 잘 동작하는 것은 아닌데, E-step 혹은 M-step의 optimization 문제를 푸는 것이 어려운 상황이 그러하다. E-step은 posterior를 계산하는 과정이므로 크게 문제가 되는 경우는 많지 않지만, M-step은 θ에 대한 optimization 문제를 풀어야하는 과정인데, 이 과정에서 문제가 발생하는 경우가 많다. 예를 들어 모든 θ를 한 번에 jointly optimize하는 것이 어려워 또 다른 alternative method를 사용해야할 수 도 있다. 그렇게 되면 iterative 알고리즘 안에 nested iterative 알고리즘이 발생하게 되어 전체 알고리즘의 수렴 속도가 매우 느려지게 된다. 가장 단순하게 이 문제를 해결하는 방법으로는 nested iterative 알고리즘을 완전히 푸는 것이 아니라, 수렴 여부와 관계없이 iteration을 조금만 돌리고 다시 E-step을 구하고, 다시 M-step을 정확히 푸는 대신 iteration을 몇 번만 돌리는 등의 방식이 있을 것이다. 일반적인 경우에는 이런 방식이 수렴하지 않지만, 몇몇 경우에는 이런 방식이 local optimum에 수렴한다는 것이 증명되어 있다. 가장 대표적인 예가 RBM을 푸는 Contrastive Divergence이다.
28. Particle filter
입자를 기반으로 한 칼만 필터의 한 종류이다. 칼만 필터에는 parametric 필터와 non-parametric 필터가 존재하는데, parametric 필터는 시스템 모델이나 측정 모델을 모델링 할 때, 상태와의 관계가 선형인 경우나, 어떤 함수로 표현하여 함수의 parameter들로 써 표현을 하는 칼만 필터이다. 기본적인 칼만 필터, EKF, Unscented KF, Information filter 등이 이것에 속한다. Non-parametric 필터의 경우, parameter가 없고, 어떤 샘플들의 정보를 가지고 반복적으로 원하는 샘플을 찾아 가는 프로세스이다. 여기에는 Histogram filter particle filter 등이 있다. Particle filter 문제는 비선형성이 너무 커서 예측하기 어렵고, 기존에 상태나 측정치 등에 대한 확률 정보가 없을 때 사용한다. 예를 들어 localization 같은 문제에서 자주 사용된다.
상태에 대해 모든 가능한 위치들 중 몇몇을 샘플링 한다. 이때 샘플링 된 위치들의 값들이 초기 시간에서의 상태이다. 이 샘플들을 particle이라고 부르고, u(액션)을 통해 샘플들 중 액션에 영향을 받는 샘플들을 추려낸다. 이제 추려낸 샘플들 중 z(측정값)을 통해 importance sampling을 실시하여 측정된 위치 값들이 기존의 샘플들 중에서 겹친값들에게 겹친 확률만큼의 weight를 준다. 이러 과정을 계속 반복하여 결과를 도출한다.
1. Ransom sample 생성
2. Sampling 과정
3. Importance sampling 과정
4. Weighted samples를 찾음
5. Resampling 과정
6. 위 과정을 반복적으로 수행하여 위치를 추적함
29. Face detection
얼굴 검출(face detection)은 컴퓨터 비전의 한 분야로 영상에서 얼굴이 존재하는 위치를 알려주는 기술이다.
초기 얼굴 검출에 사용된 feature는 영상에서 얼굴의 intensity였다. 하지만 인종, 조명 등에 따라 성능이 좌우됨에 따라 이에 무관한 feature가 필요하게 되었다. 이후로 Haar-like feature를 사용하였고, 이후로 Local Binary Pattern(LBP), Modified Census Transform등의 특징이 제안되었다.
얼굴 검출을 위한 접근방법
(1) 통제된 배경 이미지에서의 얼굴탐지 : 평면의 단색 배경 이미지를 이용하거나 사전에 정의된 고정 배경 이미지를 이용.
(2)얼굴색에 의한 탐지 : 얼굴 영상을 찾기 위해 전형적인 피부색을 이용하므로 실시간 구현이 가능하고 제한된 환경에서는 좋은 성능을 보이므로 가장 널리 쓰이고 있다. 다양한 피부색과 조명조건 하에서 매우 강인하지 못하다는 단점이 있다.
(3)움직임에 의한 얼굴 탐지 : 실시간 비디오를 이용하여 움직이는 얼굴영역을 단순히 계산하는 방법. 배경에서 다른 대상물이 움직이는 경우 문제 발생.
(4)제약 없는 장면에서의 얼굴 탐지 : 흑백 이미지에서 인간처럼 얼굴을 정확히 탐지하는 알고리즘으로 통계적 클러스터 정보를 이용하는 신경 회로망 접근방법.
https://ko.wikipedia.org/wiki/%EC%96%BC%EA%B5%B4_%EA%B2%80%EC%B6%9C
얼굴 검출 - 위키백과, 우리 모두의 백과사전
얼굴 검출(face detection)은 컴퓨터 비전의 한 분야로 영상(Image)에서 얼굴이 존재하는 위치를 알려주는 기술이다. 얼굴 검출의 알고리즘적인 기본 구조는 Rowley, Baluja 그리고 Kanade의 논문 [1] 에 의해
ko.wikipedia.org
30-(1). PCA
PCA(Principal Component Analysis)는 분포된 데이터들의 주성분을 찾아주는 방법이다.

예를 들어 2차원에서 PCA는 2차원 좌표평면에 n개의 점 데이터 (x1, y1), (x2, y2), … (xn,yn)들이 분포되어 있을 때 데이터들의 분포 특성을 e1, e2 2개의 벡터로 데이터 분포를 설명해주는 것이다. e1, e2의 방향과 크기를 알면 이 데이터 분포가 어떤 형태인지를 가장 단순하면서도 효과적으로 파악할 수 있다.
PCA는 데이터 분포의 주 성분을 분석해 주는 방법이고, 주성분이란 그 방향으로 데이터들의 분산이 가장 큰 방향벡터를 의미한다.
PCA를 이용한 face recognition
얼굴 이미지의 픽셀 밝기값을 이용하여 픽셀마다 한 차원의 벡터로 만들고, 여러 개의 이미지를 통해 각 차원에 대한 주성분 벡터들을 얻는다. 이렇게 얻어진 주성분 벡터들을 다시 이미지로 해석한 것이 eigenface이다.
모든 사람의 얼굴 샘플을 모을 필요가 없고 인식 대상이 되는 사람들의 얼굴 샘플들만을 모은다. 이들 샘플들에 대해 PCA를 통해 k개의 주요 eigenface들을 구한 후 각 개인들을 eigenface로 근사했을 때의 근사 계수를 저장한다. 이후 입력 데이터가 들어왔을 때 이를 k개의 eigenface로 근사한 근사계수가 미리 저장된 개인별 근사계수들 중 누구와 가장 가까운지를 조사하여 x를 식별한다.
http://darkpgmr.tistory.com/110
[선형대수학 #6] 주성분분석(PCA)의 이해와 활용
주성분 분석, 영어로는 PCA(Principal Component Analysis). 주성분 분석(PCA)은 사람들에게 비교적 널리 알려져 있는 방법으로서, 다른 블로그, 카페 등에 이와 관련된 소개글 또한 굉장히 많다. 그래도 기
darkpgmr.tistory.com
30-(2). LDA
LDA(Linear Discriminant Analysis)란 클래스간 분산(between-class scatter)과 클래스내 분산(within-class scatter)의 비율을 최대화하는 방식으로 데이터에 대한 특징 벡터의 차원을 축소하는 방법이다.

위의 그림에서 왼쪽 그림이 오른쪽 그림보다 판별하기 용이한 이유는, 같은 클래스에 속하는 데이터들은 중심을 기준으로 서로 가까이 모여 있으며, 또한 각 클래스의 중심 간의 거리가 멀리 떨어져 있기 때문이다. 이와 같이 LDA는 가능한 클래스간의 분별 정보를 최대한 유지시키기 위해서, 특징 공간상에서 클래스 분리를 최대로 하는 주축을 기준으로 사상시켜 차원을 축소하는 방법이다.

위의 왼쪽 그림과 같이 3개의 클래스를 형성하는 2차원 데이터가 있을 경우에 여러 가지 변환행렬을 통해 1차원 부공간으로 사상시켜 차원을 축소하는 것이 가능하다. 예를 들어 최악의 1D 부공간으로 축소된 경우에는 1차원 상에서 빨강, 파랑, 초록의 데이터가 모두 혼합된 형태이기 때문에 클래스 간의 판별이 어렵다. 하지만 최상의 1D 부공간으로 축소된 경우에는 비록 데이터들이 1차원 상에 존재하더라도 각 클래스의 구별이 용이하다는 것을 쉽게 확인할 수 있다. 이와 같이 클래스 간의 분리를 최대화하는 관점에서 차원을 축소하는 방법이 LDA이다.
30-(3). Eigenface
PCA가 face recognition에서 활용되는 개념이 eigenface이다.
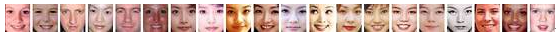
다음과 같은 20개의 45x40 얼굴 이미지들이 있다고 하자. 이미지에서 픽셀 밝기값을 일렬로 연결하여 벡터로 만들면 이들 각각의 얼굴 이미지는 45x40 = 1800차원의 벡터로 생각할 수 있다.(즉, 각각의 이미지는 1800차원 공간에서 한 점에 대응).
이제 이 20개의 1800차원 점 데이터들을 가지고 PCA를 수행하면 데이터의 차원 수와 동일한 개수의 주 성분 벡터들을 얻을 수 있다. 이렇게 얻어진 주성분 벡터들을 다시 이미지로 해석한 것이 eigenface이다. 실제 위 이미지에 대해 얻어진 1800개의 eigenface들 중 분산이 큰 순서대로 처음 20개를 나열하면 아래 그림과 같다.

위 그림에서 볼 수 있듯이 앞부분 eigenface들은 데이터들에 공통된 요소(얼굴의 전반적인 형태)를 나타내고 뒤로 갈수록 세부적인 차이 정보를 나타낸다. 그리고 더 뒤로 가면 거의 노이즈성 정보를 나타낸다.
모든 사람의 얼굴 샘플을 모을 필요가 없고 인식 대상이 되는 사람들의 얼굴 샘플들만을 모은다. 이들 샘플들에 대해 PCA를 통해 k개의 주요 eigenface들을 구한 후 각 개인들을 eigenface로 근사했을 때의 근사 계수를 저장한다. 이후 입력 데이터 x가 들어왔을 때 이를 k개의 eigenface로 근사한 근사계수가 미리 저장된 개인별 근사계수들 중 누구와 가장 가까운지를 조사하여 x를 식별한다.
'DeepLearning' 카테고리의 다른 글
| [DeepLearning] DeepFake(deepfacelab) 구글 Colab에서 개발하기 (2) | 2021.08.01 |
|---|---|
| Computer Vision Summary | 컴퓨터 비전 총정리 -4 (0) | 2021.07.12 |
| Deep Learning | GAN (Generative Adversarial Network) (0) | 2021.07.05 |
| Deep Learning | Autoencoder (0) | 2021.07.05 |
| Deep Learning | CNN (Convolutional Neural Network) (0) | 2021.07.05 |




댓글