11. Homography, Affine warping
Affine transformation은 직선, 길이(거리)의 비, 평행성(parallelism)을 보존하는 변환이며 그 일반 식은 다음과 같고, homogeneous 형태로 표현한 식은 그 오른쪽에 나타냈다.

즉, Affine 변환은 회전, 평행이동, 스케일 뿐만 아니라 shearing, reflection까지 포함한 변환이다. Affine 변환의 자유도는 6이고, 3쌍의 매칭 쌍이 있으면 affine 변환을 유일하게 결정할 수 있다. 임의의 세 점 (x1, y1), (x2, y2), (x3, y3)를 (x1’ y1’), (x2’, y2’), (x3’, y3’)로 매핑시키는 affine 변환은 위의 식을 전개하여 a,b,c,d,e,f 에 대해 묶은 후 세 점을 대입하여 얻을 수 있다. 물론 매칭쌍이 3개 이상인 경우에는 pseudo inverse를 이용하여 affine 변환을 구할 수 있다.
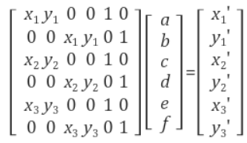
Planer surface 물체의 경우에는 3d 공간에서 2d 이미지로의 임의의 원근투영변환(perspective projective transformation)을 두 이미지 사이의 homography로 모델링할 수 있습니다. 즉, 어떤 planar surface가 서로 다른 카메라 위치에 대해 이미지 A와 이미지 B로 투영되었다면 이미지 A와 이미지 B의 관계를 homography로 표현할 수 있다는 것이다. Homography는 homogeneous 좌표계에서 정의되며 그 일반식은 다음과 같다.

Homography는 자유도가 8이며, 따라서 homography를 결정하기 위해서는 최소 4개의 매칭쌍을 필요로 한다. Homography의 자유도가 9가 아니라 8일 이유는 (x, y, 1), (wx’, wy’ w)이 homogeneous 좌표이므로 homography의 scale을 결정할 수 없기 때문이다.
12-(1). SIFT
SIFT는 영상에서 코너점 등 식별이 용이한 특징점들을 선택한 후에 각 특징점을 중심으로한 로컬 패치(local patch)에 대해 아래와 같은 특징 벡터를 추출한 것을 말한다.

SIFT 특징벡터는 특징점 주변의 영상패치를 4x4 블록으로 나누고 각 블록에 속한 픽셀들의 gradient 방향과 크기에 대한 히스토그램을 구한 후 이 히스토그램 bin 값들을 일렬로 쭉 연결한 128차원 벡터이다.
SIFT는 기본적으로 특징점 주변의 로컬한 gradient 분포특성(밝기 변화의 방향 및 밝기 변화의 급격한 정도)을 표현하는 feature이다. SIFT를 포함한 SURF, ORB 등의 local feature들은 대상의 크기변화, 형태변화, 방향(회전)변화에 강인하면서도 구분력이 뛰어나다.
12-(2). SURF
SURF(Speeded-Up Robust Features)는 scale space 상에서 Hessian 행렬의 행렬식(determinant)이 극대인 점들을 특징점으로 검출한다. SURF에서 사용한 특징점 추출방법을 Fast Hessian이라 부른다. SIFT는 DoG로 LoG를 근사하는 방법을 사용했지만 SURF는 박스 필터로 LoG를 근사하는 방법을 사용한다. SURF는 블러이미지나 회전된 이미지의 경우 이미지의 특징을 제대로 잡아내지만, 뷰포인트가 바뀌어 있거나 조명이 달라진 상태에서는 이미지 특징을 제대로 검출하지 못한다.
속도 향상을 위해 SURF가 제안한 방법은 요약하면 3가지 이다.
1. Integral image
SURF에서는 특징점 계산을 위해 고속 헤시안 검출을 사용하는데, 이 때 적분 영상을 사용한다. 적분 영상은 영상이 갖는 영역의 넓이(밝기의 합)을 구하는 것이다. 영상 밝기의 합을 매번 계산할 경우 n^2으로 연산속도가 매우 느리지만, 적분 영상을 처음에 하나 만들어 두고 영상의 부분합을 구하면(3번의 더하기, 빼기 연산) 빠른 속도로 계산할 수 있다.
2. 축소한 detector와 descriptor를 사용하여 빠른 (차원 수 축소)
특징점을 계산하기 위해 SURF는 헤시안 행렬을 사용한다. 정확성이 좋고 determinant가 최대값인 위치의 blob 구조를 검출하기 위해서라고 논문에 나와있다. 만약 determinant가 음수이고 eigenvalue가 서로 다른 부호이면 해당 좌표는 특징점이 아니고, determinant가 양수이고 eigenvalue가 둘 다 음수 혹은 양수이면 해당 좌표는 특징점으로 판단한다.
또한 가우시안 분포 헤시안 행렬을 계산할 때 계산을 좀 더 단순화시키기 위해 근사화한 Dxx와 Dyy 박스필터를 사용한다.

위 그림과 같이 근사화한 박스필터를 사용하므로써 적분이미지 계싼으로 영역의 넓이를 빠르게 구하고, 구한 넓이로 헤시안 행렬을 계산해 특징점을 판단한다.
SIFT는 필터 사이즈를 고정시키고, 이미지 사이즈를 줄여 관심점을 검출하는 반면, SURF는 SIFT와 반대로 이미지 스케일을 고정시키고 필터 사이즈를 키워가며 관심점을 추출한다. 적분 이미지를 사용하기 때문에 위치를 변경하는 것만으로 필터 사이즈를 조절할 수 있고, down sampling을 하지 않기 때문에 aliasing이 없다는 장점이 있다.
Contrast에 invariant하다는 것을 보여주기 위해 단순히 x, y 축에 대한 response값을 합한 것이 아니라, 각 값에 대한 절대값을 합하여 contrast에 강하다는 것을 증명하고 있다.

3. Contrast를 이용한 빠른 매칭
Hessian 행렬을 계산한 라플라시안 부호를 비교해 간단히 매칭을 시도한다. (부호만 비교)
12-(3). HOG
HOG(Histogram of Oriented Gradient)는 대상 영역을 일정 크기의 셀로 분할하고, 각 셀마다 edge 픽셀(gradient magnitude가 일정 값 이상인 픽셀)들의 방향에 대한 히스토그램을 구한 후 이들 히스토그램 bin 값들을 일렬로 연결한 벡터이다. 즉, HOG는 edge의 방향 히스토그램 템플릿으로 볼 수 있다.
템플릿 매칭의 경우에는 원래 영상의 기하학적 정보를 그대로 유지하며 매칭할 수 있지만, 대상의 형태가 위치가 조금만 바뀌어도 매칭이 잘 안되는 문제가 있다. 반면에 히스토그램 매칭은 대상의 형태가 변해도 매칭을 할 수 있지만, 대상의 기하학적 정보를 잃어버리고 단지 분포 정보만을 기억하기 때문에 잘못된 대상과도 매칭이 되는 문제가 있다. HOG는 템플릿 매칭과 히스토그램 매칭의 중간 단계에 있는 매칭 방법으로 볼 수 있으며 블록 단위로는 기하학적 정보를 유지하되, 각 블록 내부에서는 히스토그램을 사용함으로써 로컬한 변화에는 어느정도 강인한 특성을 가지고 있다.
또한 HOG는 edge의 방향정보를 이용하기 때문에 일종의 edge기반 템플릿 매칭 방법으로도 볼 수 있다. Edge는 기본적으로 영상의 밝기 변화, 조명 변화 등에 덜 민감하므로 HOG 또한 유사한 특성을 갖는다고 생각할 수 있다. 또한 HOG는 물체의 실루엣(윤곽선) 정보를 이용하므로 사람, 자동차 등과 같이 내부 패턴이 복잡하지 않으면서도 고유의 독특한 윤곽선 정보를 갖는 물체를 식별하는데 적합한 영상 feature이다.
HOG를 SIFT와 비교해보면, HOG는 일종의 템플릿 매칭이기 때문에 물체가 회전된 경우나 형태변화가 심한 경우에는 검출이 힘들지만 SIFT는 모델의 특징점과 입력 영상의 특징점에 대해 특징점 단위로 매칭이 이루어지기 때문에 물체의 형태변화, 크기변화, 회전 등에 무관하게 매칭이 이루어질 수 있다. 이러한 특성에 비추어 보았을 때 HOG는 물체의 형태변화가 심하지 않고 내부 패턴이 단순하며 물체의 윤곽선으로 물체를 식별할 수 있는 경우에 적합하고, SIFT는 내부 패턴이 복잡하여 특징점이 풍부한 경우에 적합한 방법이다.
13. Hough transform
영상에서 직선검출의 기법중의 하나이다. (Edge 검출->)영역변환->thresholding 순으로 진행된다. Preprocessing 과정인 edge 검출은 canny, sobel등의 방법을 이용하여 수행한다. 이 결과로 얻은 binary혹은 grey image(0이면 non-edges, 1이상이면 edges)를 이용하여 hough transform을 수행한다.
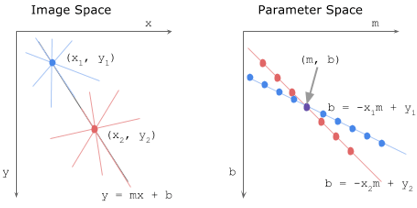
영역변환(transform)과정은 먼저 (x, y)좌표계에 존재하는 영상을 새로운 좌표계로 변환한다. 새로운 좌표계 (a, b)는 직선의 방정식 y=ax+b의 기울기 a와 y절편 b로 이루어진 좌표계이다. (x, y)공간에서 (a, b)공간으로 변환하게 되면 하나의 점이 직선을 나타내게 된다.
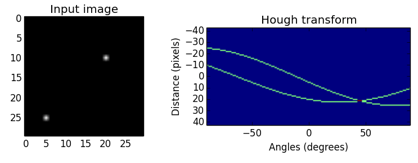
허프변환은 평범히 y=ax+b로 표현되는 직선의 방정식을 사용하지 않고 r=x cos theta + y sin theta의 식을 사용한다. 그 이유는 기울기가 무한대인 경우를 방지하기 위함이다. 즉, (a, b) 공간이 아닌 (rho, theta) 공간을 사용한다.
각 edge의 점과 각 theta에 대해 가장 가까운 rho값을 찾고 그 index를 증가시킨다. 각 요소는 매개 변수 (rho, theta)를 가진 가능성을 가진 “선” 후보에게 얼마나 많은 점(픽셀)이 투표했는지 알려준다. (rho, theta) 좌표계에서 특정 임계치 이상을 직선으로 뽑게 되는데, 영상에서 적당한 임계치를 이용해 원하는 직선을 뽑는 것은 매우 어렵다. 따라서 Local Maxima를 이용해 중복될 수 있는 선들을 제거하는 방법이 많이 사용된다.
14. RANSAC
RANSAC(RANdom Sample Consensus)는 무작위로 샘플 데이터들을 뽑은 다음에 최대로 consensus가 형성된 결과를 선택하는 것이다. 최소자승법(least square method)은 데이터들과의 residual의 제곱의 합을 최소화하도록 모델을 찾지만, RANSAC은 consensus가 최대인, 즉 근사된 모델 근방에 있는 데이터들이 어느 쪽이 많은지 확인해 보면 된다. RANSAC은 관측 데이터에 outlier가 많더라도 데이터 근사가 가능하다는 점이 장점이다. 여기서 outlier는 데이터의 분포에서 현저하게 벗어나 있는 관측값을 말한다.

RANSAC은 일단 무작위로 샘플 데이터 몇 개를 뽑아서 이 샘플 데이터들을 만족하는 모델 파라미터를 구한다. 이렇게 구한 모델과 가까이에 있는 데이터들의 개수를 세어서 그 개수가 크다면 이 모델을 기억해 둔다. 이러한 과정을 N번 반복한 후 가장 지지하는 데이터의 개수가 많았던 모델을 최종 결과로 반환한다. RANSAC 알고리즘을 돌리기 위해서는 크게 2가지의 파라미터를 결정해야 한다. 샘플링 과정을 몇 번 반복할 것(N)인지, 그리고 inlier와 outlier의 경계(T)를 어떻게 정할 것인지 이다. RANSAC이 성공하기 위해서는 N번의 시도 중 적어도 한번은 inlier들에서만 샘플 데이터가 뽑혀야 한다. 이러한 확률은 N을 키우면 키울수록 증가하지만 무한정 RANSAC을 돌릴 수는 없기 때문에 보통은 확률적으로 반복 횟수를 결정한다. RANSAC 반복횟수를 N, 한번에 뽑는 샘플 개수를 m, 입력 데이터 중에서 inlier의 비율을 α라 하면, N번 중 적어도 한번은 inlier에서만 샘플이 뽑힐 확률 p는 다음과 같다. 그리고 α와 m을 알고, 원하는 p를 알면, N을 구할 수 있다.

RANSAC은 지지하는 데이터 개수가 가장 많은 모델을 뽑은 파라미터 추정 방법이다. 데이터 (xi, yi)와 모델 f와의 거리 ri = | yi – f(xi) | 가 T 이하이면, 그 모델을 지지하는 데이터로 간주한다. 즉, 먼저 RACSAC을 적용하고자 하는 실제 문제에 대해서 inlier들로만 구성된 실험 데이터들을 획득하고, inlier 데이터들에 대해서 최소자승법을 적용하여 가장 잘 근사된 모델을 구한다. 이렇게 구한 모델과 inlier들과의 residual (ri = yi – f(xi))들을 구한 후, 이들의 분산(또는 표준편차)을 구해서, 이에 비례하게 T를 결정한다. inlier들의 residual이 정규분포를 따른다고 가정했을 때, T = 2σ로 잡으면 97.7%, T = 3σ로 잡으면 99.9%의 inlier들을 포함하게 된다.
T를 정하는데 있어서 어려운 문제는 inlier들의 분산이 동적으로 변하는 경우이다. 이러한 경우에는 T를 데이터마다 유동적으로 결정해주어야 하는데 RANSAC에서는 이러한 문제를 adaptive threshold또는 adaptive sacle문제라고 부르며, N을 adaptive하게 하는 것과 T를 adaptive하게 하는 두 가지로 나뉜다.
15. Corner detection
영상에서 물체를 추적하거나 인식할 때, 영상과 영상을 매칭할 때 사용하는 가장 일반적인 방법은 영상에서 주요 특징점(keypoint)를 뽑아서 매칭하는 것입니다. 좋은 영상 특징점이 되기 위한 조건은 다음과 같습니다.
1. 물체의 형태나 크기, 위치가 변해도 쉽게 식별이 가능할 것
2. 카메라의 시점, 조명이 변해도 영상에서 해당 지점을 쉽게 찾아낼 수 있을 것
영상에서 이러한 조건을 만족하는 가장 좋은 특징점은 바로 코저머(corner point)입니다. 그리고 대부분의 특징점 추출 알고리즘들은 이러한 코너점 검출을 바탕으로 하고 있습니다.
영상에서 코너점을 찾는 가장 대표적인 방법은 1988년에 발표된 harris corner detector입니다. 영상에서 코너를 찾는 기본적인 아이디어는 아래 그림과 같이 영상에서 작은 윈도우를 조금씩 이동 시켰을 때, 모든 방향으로 영상 변화가 커야 한다는 것입니다.

코너점을 찾기 위해서는 먼저, (Δx, Δy)만큼 윈도우를 이동시켰을 때 영상의 SSD(Sum of Squared Difference) 변화량 E는 다음과 같습니다. (W: 로컬 윈도우)

Shift값 (Δx, Δy)이 매우 작다고 가정하고 gradient를 이용하여 I를 선형 근사하면(Taylor 근사),
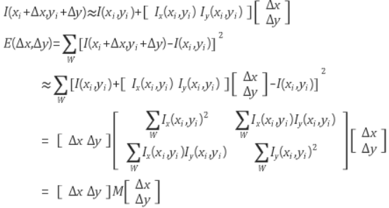
가 된다. 이 때, 2x2 행렬 M의 두 eigenvalue를 λ1, λ2 (λ1≥λ2)라 하면, 영상 변화량 E는 윈도우를 λ1의 고유벡터(eigenvector) 방향으로 shift 시킬 때 최대가 되고, λ2의 고유벡터 방향으로 shift시킬 때 최소가 된다. 또한 두 고유값(eigenvalue) λ1, λ2는 해당 고유벡터 방향으로 실제 영상 변화량(E) 값이 된다.
따라서, M의 두 고유값 λ1, λ2를 구했을 때, 두 값이 모두 큰 값이면 코너점, 모두 작은 값이면 flat한 지역, 하나는 크고 다른 하나는 작은 값이면 edge 영역으로 판단할 수 있다. 실제 harris 방법에서는 M의 고유값을 직접 구하지 않고 det(M)= λ1 λ2, tr(M)= λ1+ λ2임을 이용하여 다음 수식의 부호로 코너점 여부를 결정한다.

즉, R>0이면 코너점, R<0이면 edge, |R|이 매우 작은 값이면 R 부호에 관계없이 flat으로 판단한다. (여기서 k는 경험적 상수로서 0.04 ~ 0.06 사이의 값)
Harris corner 검출 방법의 특징은, 영상의 평행이동, 회전변화에 불변이고 affine 변화, 조명 변화에도 어느 정도는 강인하다. 하지만 영상의 크기 변화에는 영향을 받기 때문에 응용에 따라서는 여러 영상 스케일에서 특징점을 뽑을 필요가 있다.
16. Sliding Window
Sliding window 기법은 영상에서 물체를 찾는데 가장 기본적으로 사용되는 기법으로서, 영상에서 윈도우를 일정한 간격으로 이동시키면서 윈도우 내의 영상 영역이 찾고자 하는 물체인지 아닌지를 판단하는 방법이다. 찾고자 하는 물체가 영상내 어떤 위치와 어떤 크기로 있는지를 모르기 때문에 가능한 모든 영상 위치 및 크기에 대해 물체의 존재 여부를 반복적으로 검사하는 exhaustive searching 방법이 sliding window 기법의 본질이다.

Sliding window 기법에서는 어떤 평가함수 f가 윈도우 영역(r)마다 (f)값을 조사하여 임계값(threshold value) 이상이면 대상 물체가 있는 것으로 판단한다.
이러한 sliding window 탐색은 거의 모든 영상 물체 탐색(object localization) 방법들에서 공통적으로 사용하고 있지만 그 엄청난 반복 검사로 인해 알고리즘의 속도를 현저히 느리게 하는 가장 큰 주범이기도 하다.
가장 대표적인 Sliding window detector로는 Viola-jones가 있다. 비슷하지 않은 윈도우는 빠르게 제거하는 것과 연산이 빠른 특징들을 사용하여 매우 빠른 성능을 보인다. 전자를 Cascade 방식이라고 하는데, 각 stage에서 threshold와 비교해서 낮을 경우 다음 stage로 가지 않고 바로 검사를 끝낸다. 앞 단의 Stage에서 많이 걸러낼 수 있다면 그 성능은 극대화된다. Viola-jones 방법에서 사용하는 연산이 빠른 특징은 Haar-like features이다. 2개 이상의 사각형의 조합으로 이루어진 feature로 -1과 +1의 값을 가진 filter이다. 다양한 위치와 스케일에 대해 feature를 적용하여 연산한다. 그 외에 integral image, adaboost를 이용한 feature selection 방법도 속도를 높이는데 매우 중요한 역할을 한다.

17. Template Matching
템플릿 매칭은 어떤 이미지에서 부분 이미지를 검색하고 찾는 방법이다. 여기에서 말한 부분 이미지를 템플릿 이미지라고 부른다. 템플릿 이미지의 중심을 (x, y)라 하고, 템플릿 이미지를 타겟이미지 위에 두고 템플릿 이미지로 덮인 타겟 이미지 부분의 픽셀값과 템플릿 이미지의 픽셀값을 특정 수학 연산으로 비교한다. 이 값을 R(x, y0라 한다. 이와 같은 방법으로 타겟 이미지 전체를 미끄러져가면서 비교한 결과인 R(x, y) 전체는 테두리 부분 때문에 타겟 이미지보다 작은 이미지가 된다.
템플릿 이미지와 타겟 이미지를 비교하기 위한 연산 방법은 다양하다. 대표적으로 Sum of Squared Differences(SSD), normalized SSD, Sum of Absolute Differences(SAD), cross correlation이 있다. R(x, y)의 최대값, 최소값, 그리고 그 위치를 템플릿 매칭의 결과로 얻는다. 타겟 이미지를 비교 연산하는 방법에 따라 최대값이 원하는 값일 수도 있고, 최소값이 원하는 값일 수도 있다.

18. Scale invariant recognition
우리는 동일한 장면을 보면서도 스케일에 따라서는 전혀 다른 것들을 보게 된다. 예를 들어, 똑같은 나무에 대하여 작은 스케일에서는 나뭇잎이나 가지를 보겠지만, 큰 스케일로는 나무가 포함된 숲을 볼 수 있다. 영상에서 물체의 특징을 계산할 때 어떤 스케일에서 보느냐에 따라 전혀 다른 결과가 나올 수 있기 때문에 recognition 분야에서 스케일은 매우 중요한 문제 중 하나이다. 영상의 코너 검출에서, 아래 그림과 같은 형태의 물체는 큰 스케일(오른쪽)에서는 명확히 코너점으로 인식되겠지만, 작은 스케일(왼쪽)에서는 완만한 곡선 또는 직선으로 밖에 인식되지 못할 것이다.

이러한 스케일 문제에 있어서 가장 근원적인 해결책은 대상을 여러 스케일에 걸쳐 표현(multi-scale representation)하고 분석하는 것이다. 영상처리 분야에서는 이미지 스케일을 다루는 방법으로 크게 image pyramid 방법과 scale-space theory 방법이 있다.
입력 이미지의 크기를 단계적으로 변화(축소)시켜 생성한 일련의 이미지 집합을 이미지 피라미드라고 한다.

예를 들어 영상에서 보행자를 검출하는 경우, 대상 이미지의 이미지 피라미드를 생성한 후 각 스케일 영상에서 고정된 크기의 윈도우를 이동시켜 가면서 윈도우 내 영역을 검사하는 방법이 일반적이다.
가우시안 피라미드를 만드는 경우도 있다. 이미지 피라미드를 생성할 때, 일련의 blurring과 sub sampling을 통해 이미지를 축소시켜 가면서 피라미드를 생성하는 경우도 있다. 블러링과 1/2 축소과정을 반복시켜 가며 이루어진다. 블러링에서는 Gaussian 필터를 이용하고, 다운 샘플링은 짝수번째 픽셀들은 버리고 홀수번째 픽셀들만 취하는 방식으로 이루어진다. 가우시안 피라미드에서는 이미지의 크기가 바르게 줄어들기 때문에 피라미드를 구축하기 위한 시간과 메모리 요구량이 낮고 이후 빠른 영상분석이 가능한 장점을 갖는다. 하지만 스케일 축에서 보면 가우시안 피라미드는 물체가 가질 수 있는 연속된 스케일 변화를 매우 coarse하게만 샘플링한 것이기 때문에 스케일 축 상에서 물체를 비교하거나 매칭할 때 알고리즘적으로 문제가 어려워지는 단점을 갖는다. 따라서 가우시안 피라미드는 축소된 이미지에서 빠르게 원하는 특징이나 대상을 검출한 후에 점차적으로 원래 스케일에서 보다 정확한 특징을 계산하는 coarse-to-fine 형태로 주로 사용된다. Lucas-Kanade optical flow 알고리즘에서 이러한 방식을 사용한다.
Scale space는 스케일 축을 따라서 생성되는 공간이다. 즉, 어떤 대상을 볼 때 하나의 스케일 또는 현재의 스케일 만을 보는 것이 아니라 대상이 가질 수 있는 다양한 스케일 범위를 한꺼번에 표현하는 공간이다. Scale space 이론은 대상을 (스케일 축이 파라미터로 하는) 공간상의 한 점으로 표현한다. 이미지의 경우 이미지 f(x, y)에 대한 scale space 표현은 Gaussian blurring을 통해 생성되는 일련의 스무딩된 이미지 fσ(x, y)들로 정의된다.

식 (1)에서 scale parameter σ는 convolution에서 사용된 Gaussian filter의 표준편차에 해당하며, σ=0일 때, fσ(x, y)=f(x, y)로 정의된다. 이미지를 직접 확대, 축소시키지 않고도 스케일을 변화시키는 방법이 바로 이미지를 블러링시키는 것이다. 이미지를 블러링시킬수록 세부적인 detail이 사라지고 보다 큰 스케일에서의 이미지 구조를 파악할 수 있게된다. 블러링된 이미지의 스케일은 사용된 Gaussian filter의 σ에 비례한다. 만일 σ2 = kσ1이라면, fσ2(x, y)의 스케일은 fσ1(x,y)의 스케일의 k배가 된다.
Scale space 자체는 연속적으로 정의되지만 현실적으로 모든 스케일에 대해 분석하는 것은 불가능하다. 따라서 scale space를 영상처리에 활용하기 위해서는 스케일 축을 따라서 일정한 간격으로 샘플링 된 scale space를 생성해야 한다. 이 때의 샘플링 간격을 scale step이라 부르는데 보통 루트 2를 사용한다.

scale space를 생성할 때, 메모리의 효율성과 연산의 효율성을 위해서 Gaussian 블러링과 다운 샘플링을 혼용하여 사용하는 것이 일반적이다. Gaussian 필터를 단계적으로 적용하여 이미지의 스케일을 증가시켜 가다가 스케일이 2배가 되는 시점에서 1/2 크기로 다운 샘플링한다. 이후 다운 샘플링된 이미지에서 다시 Gaussian 필터를 적용해 가는 방식이다. 이 때, 스케일이 2배까지 Gaussian 블러링으로 생성되는 스케일 공간을 octave라고 부르며 scale step이 작을수록 한 octave를 구성하는 이미지의 개수가 많아진다.
Scale space를 구축하는 목적은 다양한 스케일에 걸쳐서 이미지 특성을 분석하기 위함이다. 그런데 scale space 이미지에 직접 어떤 연산자를 적용하는 것은 문제가 있다. Scale space 이론에 의해 생성되는 이미지들은 기본적으로 블러링만 되어 있을 뿐 원래 이미지와 resolution은 동일하다. 따라서 스케일별 특성을 분석하는 것이 목적이기 때문에 모든 이미지에 고정 크기의 연산자를 적용하는 것은 적합하지 않다. 또한 스케일이 원본이미지의 정수배인 경우에는 다운 샘플링된 이미지에 연산자를 적용하면 되지만 정수배가 아닌 경우에는 이러한 적용도 쉽지 않다.
scale space가 활용되는 방식은 고정된 크기의 연산자를 모든 스케일의 이미지에서 동일하게 적용하는 것이다. 그리고 이러한 연산자로는 gradient, laplacian, hessian 등과 같은 1차 또는 2차 미분을 기반으로 한 연산자가 주로 이용된다.
미분 연산자는 영상의 밝기변화 특성을 분석하기 위한 연산자로서 edge 검출에 사용되는 sobel 필터 등이 대표적인 미분 연산자이다. 그런데, 미분 연산자는 블러링된 이미지에 미분을 적용하는 것과 Gaussian 필터에 미분을 적용한 후 블러링시키는 것이 동일한 결과를 갖는 매우 좋은 특성을 가지고 있다. 즉, scale space 상의 이미지들에 직접 미분 연산자를 적용시키는 것과 Gaussian 필터에 미분을 적용한 후 convolution하는 것이 동일하다는 것이다. 전자는 ill-posed problem이지만 후자는 well-posed problem이다. 또한 직접 미분을 구하지 않고 Gaussian 필터에 미분을 적용한 후 블러링시키는 것이 계산상으로도 이득이다. 그리고 이러한 성질은 1차 미분 뿐만 아니라 모든 차수의 미분에 대해 성립한다.
Edge, ridge, corner blob등과 같은 영상 feature들은 대부분 이러한 미분 연산자를 기반으로 검출될 수 있다. 따라서 실제 scale space의 주 응용은 미분 연산자를 기반으로 edge, ridge, corner, blob 등과 같은 영상 특징들을 여러 스케일에 걸쳐 분석하는 것으로 볼 수 있다.
Scale space의 가장 큰 활용은 영상에서 스케일에 불변인 특징을 뽑는 것으로 볼 수 있다. 스케일에 불변인 특징이라 하면 이미지를 어떤 스케일에서 찍었든 간에 동일한 물체 지점에 대해 계산된 영상 특징은 서로 동일해야 함을 의미한다. 그런데, 이미지의 스케일이 바뀌면 계산된 영상 특징은 당연히 바뀌기 때문에 일반적으로는 scale invariance를 만족시키기 어렵다.
그 방법은 먼저 현재 이미지 내에서뿐만 아니라 스케일 축 상에서 특징점(keypoint)을 찾은 후, 해당 특징점이 발견된 스케일 이미지에서 영상 특징을 계산하는 것이다. 이러한 영상 특징점(keypoint)으로는 카메라 시점이 바뀌어도 쉽게 반복 검출이 가능한 코너점(corner point)이 주로 사용된다(영상 특징점(keypoint) 추출방법 글 참조). 코너점을 찾는 방법에는 여러 가지가 있지만 그중 한 방법은 Laplacian이 극대 또는 극소인 점을 찾는 것이다. 즉, 이미지 내에서 뿐만 아니라 스케일 축을 따라서도 Laplacian이 극대 또는 극소가 되는 점을 찾으면 해당 점이 스케일에 불변인 특징점이 된다. 그리고 이렇게 찾아진 특징점 위치 및 스케일에서 영상 특징량(descriptor)을 계산하면 스케일에 불변인 영상 특징량이 된다. 이렇게 찾아진 특징점 및 특징량이 스케일에 불변인 이유는 입력 이미지가 어떤 스케일에서 촬영되었다 하더라도 스케일 공간 탐색을 통해서 해당 스케일을 찾아냄으로써 동일한 특징량 계산이 가능해지기 때문이다.
19. Intergral Image
적분 영상이란 쉽게 말해 다음 픽셀에 이전 픽셀까지의 합이 더해진 영상이다. 그 수식은 아래와 같다.

여기서 integralImage(x, y)는 적분 영상이고 originalImage (x’, y’)은 원래 영상이다. 적분 영상의 장점은 특정 영역의 픽셀 값의 총합을 매우 쉽고 빠르게 구할 수 있다는 점이다.
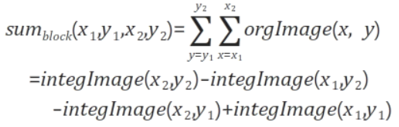
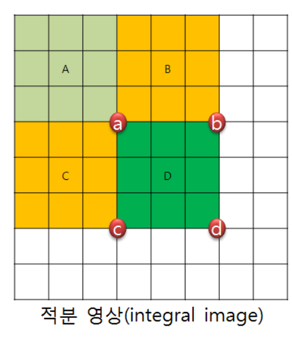
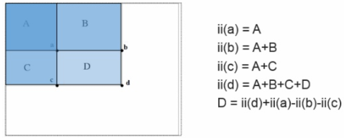
D 영역의 픽셀 값을 얻기 위해서 점 d까지의 넓이와 점 c까지의 넓이를 뺀 후 두 번 빼진 점 a까지의 넓이를 한 번 더해줌으로써 d 영역의 넓이를 구할 수 있다. 따라서 2번의 뺄셈과 한번의 덧셈 연산으로 d 영역의 넓이를 구할 수 있다.
20. Color models
색 모델은 색이 숫자로 표현될 수 있는 방법을 묘사하는 추상적인 수학적 모델이다. 보통 3, 4개의 color components로 이루어진다.
CIE XYZ color space
CIE XYZ color space는 수학적으로 정의된 최초의 color space 중 하나이다. CIE XYZ 색 공간에서 삼색 자극값인 X, Y, Z는 각각 빨강, 초록, 파랑과 비슷한 색이다. 다양한 파장을 가진 두 개의 색을 섞으면, 다른 색과 비슷하게 보일 수 있다. 이런 현상을 조건등색(metamerism)이라 한다. CIE XYZ 색 공간에서, 두 개의 색이 가진 삼색 자극값의 합은, 두 개의 색이 갖는 파장과 관계없이, 똑같이 보이는 다른 삼색의 삼색 자극값과 동일하다.
인간의 눈은 세 개의 색채 수용기를 갖고 있기 때문에, 모든 가시광선의 분포도는 3차원 도형이 된다. 그러나 색은 밝기와 색도의 두 가지 요소로 나눌 수 있다. 예를 들어, 흰색은 밝은 색이며, 회색은 동일한 흰색의 좀 더 어두운 형태로 표현할 수 있다. 즉 흰색과 회색은 밝기는 다르지만 색도는 같은 색이다.
CIE XYZ 색 공간은 Y 값이 밝기 또는 조도의 값이 되도록 설계되어 있다. 따라서 어떤 색의 색도는 두 개의 값 X, Y, Z로부터 계산된 값 x, y로 표현할 수 있다.
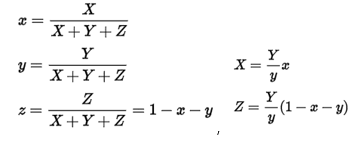
RGB color model
Additive color모델로 기본 색상(R, G, B)의 빛을 혼합하여 인간의 색 공간의 상당 부분을 차지는 모델이다. TV와 computer monitor등이 이러한 모델을 활용한다.
단점으로는, 빨간색, 녹색, 파란색이 가져야하는 색도(chromaticity) 다이어그램의 loci가 정확하게 일치하지 않으므로 동일한 RGB 값은 서로 다른 화면에서 약간 다른 색을 유발할 수 있다. 또한 R, G, B가 동일하게 직각인 세 축으로 표현된다는 것, additive만 한다는 것도 색을 표현하는 완벽한 방법이 될 수 없는 이유가 된다.
HSV and HSL represntations
휴먼 비젼, 컴퓨터 그래픽 연구진 RGB으 기하학적 모델이 인간의 시각에 의해 인식되는 색의 속성과 잘못 매칭된다고 판단하였고, 새로운 색 표현 방법인 HSV와 HSL을 제안하였다. H는 Hue, S는 Saturation, V는 value, L은 lightness를 나타낸다. HSV와 HSL은 중성 색의 중심 축을 기준으로 방사형 슬라이스에 각 색조의 색상을 배열하여 RGB의 색상 상자 표현을 향상시킨다.
CMYK color model
Subtractive 모델로, 백색 위에 Cyan, magenta, yellow 투명 염료/잉크를 조합하여 색을 구성한다. 보통 어두운 색을 만드는 성능을 높이기 위해 black 잉크를 추가한다. Cyan 잉크는 빨간색 빛을 흡수하지만 초록색과 파란색은 통과시킨다. Magenta ink는 녹색 빛은 흡수하지만 빨간색과 파란색은 통과시킨다. Yellow ink는 파란색 빛은 흡수하지만 빨간색과 초록색은 통과시킨다. 백색 판은 투과광을 관찰자에게 반사시킨다.
Lab 색 공간
CIE XYZ 색 공간을 비선형 변환하여 만들어진 색 공간이다. Lab 색 공간은 XYZ에서 정의된 흰색에 대한 상대값으로 정의되어 있다. 따라서 흰색의 값에 따라서 다른 색을 가리킬 수 있다. Lab 색 공간은 RGB나 CMYK가 표현할 수 있는 모든 색역을 포함하며, 인간이 지각할 수 없는 색깔도 포함하고 있다.
Lab 색 공간의 가장 큰 장점은 RGB나 CMYK와 달리 매체에 독립적이라는 것이다. 디스플레이 장비나 인쇄 매체에 따라 색이 달라지는 색 공간과 달리 Lab 색공간은 인간의 시각에 대한 연구를 바탕으로 정의되었다. 특히 휘도 축인 L 값은 인간이 느끼는 밝기에 대응하도록 설계되었다.
L은 밝기를 나타내며, a는 빨강과 초록 중 어느쪽으로 치우쳤는지를 나타낸다. B는 노랑과 파랑을 나타낸다. 이간의 색 지각이 비선형이라는 연구 결과에 따라 Lab 색 공간은 실제 빛의 파장과 비선형적 관계를 갖는다.

'DeepLearning' 카테고리의 다른 글
| Deep Learning | MNIST (0) | 2021.06.30 |
|---|---|
| Deep Learning | Learning Model 재사용 & 텐서보드 사용 (0) | 2021.06.30 |
| Computer Vision Summary | 컴퓨터 비전 총정리 -1 (0) | 2021.06.29 |
| Deep Learning | 기본 인공 신경망 구현 (0) | 2021.06.24 |
| Deep Learning | Linear regression(선형 회귀 모델 구현) (0) | 2021.06.17 |




댓글