반응형
문제
https://programmers.co.kr/learn/courses/30/lessons/92335
코딩테스트 연습 - k진수에서 소수 개수 구하기
문제 설명 양의 정수 n이 주어집니다. 이 숫자를 k진수로 바꿨을 때, 변환된 수 안에 아래 조건에 맞는 소수(Prime number)가 몇 개인지 알아보려 합니다. 0P0처럼 소수 양쪽에 0이 있는 경우 P0처럼 소
programmers.co.kr
풀이1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
def solution(n, k):
answer = 0
k_num = n_jinsu(n, k)
temp_list = k_num.split('0')
for i in temp_list:
if i=='':
continue
elif is_prime(i)==True:
answer += 1
return answer
def is_prime(n):
n = int(float(n))
if n<2:
return False
for i in range(2, n):
if n % i == 0:
return False # i로 나누어 떨어지면 소수가 아니므로 False 리턴
return True
def n_jinsu(n, k):
rev_base = ''
while n > 0:
n, mod = divmod(n, k)
rev_base += str(mod)
return rev_base[::-1]
|
cs |
크게 두 개의 함수 작성이 필요하다.
n을 k진수로 바꾸기 위한 n_jinsu 함수와 소수인지 검사하는 is_prime 함수를 작성했다.
n을 k진수로 바꾼 후에, 0을 기준으로 문자열을 자른다.
"00"과 같이 붙어있을 경우에 빈 문자열로 잘리기 때문에 빈 문자열인 경우는 continue하고,
아닌 경우에는 소수인지 검사한다.
2부터 n까지 늘려가며 나누었을 때, 나머지가 0이면 False를 리턴하고 개수를 늘려준다.
코드 제출 결과
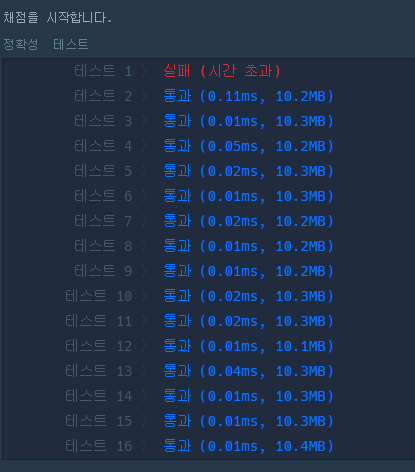
해당 코드로 제출 시 테스트 케이스 1번이 실패(시간초과)가 뜬다.
아무래도 모든 수에 대해 소수 검사를 다하기 때문에 시간초과가 나오는 것으로 판단된다.

한 가지 예시를 생각해보자.
36이라는 수는 2,4,6,9,18로 나눠진다. 이 때 숫자 5개를 전부 돌 필요가 없다.
2는 18과 짝지어지고 4는 9, 그리고 6은 6과 짝지어지기 때문이다.
따라서 n이라는 숫자를 소수판별 할 때 2~n의 제곱근까지만 판별해도 소수판별이 가능하다.
코드를 수정한 후에 채점하니 테스트1 케이스도 통과되었다.
풀이2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
def solution(n, k):
answer = 0
k_num = n_jinsu(n, k)
temp_list = k_num.split('0')
for i in temp_list:
if i=='':
continue
elif is_prime(i)==True:
answer += 1
return answer
def is_prime(n):
n = int(float(n))
if n==2 or n==3:
return True
if n<2 or n%2==0:
return False
for i in range(2, int(n**0.5)+1):
if n % i == 0:
return False # i로 나누어 떨어지면 소수가 아니므로 False 리턴
return True
def n_jinsu(n, k):
rev_base = ''
while n > 0:
n, mod = divmod(n, k)
rev_base += str(mod)
return rev_base[::-1]
|
cs |


반응형
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 체육복 파이썬 풀이 - Greedy(탐욕법) 알고리즘 (0) | 2022.05.31 |
|---|---|
| [프로그래머스] 로또의 최고 순위와 최저 순위 - 파이썬 풀이 (0) | 2022.04.29 |
| [프로그래머스][2022 카카오 블라인드 테스트] 신고 결과 받기 - 파이썬 풀이 (0) | 2022.04.26 |
| [프로그래머스] 가장 큰 수(level 2) 파이썬 문제 풀이 (2) | 2021.08.27 |
| [프로그래머스] 모의고사(level 1) 파이썬 문제 풀이 (0) | 2021.08.23 |




댓글